切切切（思维场）

题目描述

在平面直角坐标系上，有一个顶点分别在 $(x_0,y_0),(x_0+a,y_0),(x_0,y_0+b)$ 三点上的三角形 $A$ ；

请给出一条平行于 $y$ 轴的直线 $L:x=c$ ，使得三角形 $A$ 被直线分成面积相等的两半；

正式地讲：请给出一个实数 $c$ ，使得三角形 $A$ 中，横坐标小于或等于 $c$ 的点所组成图形的面积 $S_{Left}$ ，与横坐标大于 $c$ 的点所组成图形的面积 $S_{Right}$ 相等。

输入格式

输入为一行，四个整数 $x_0,y_0,a,b$ （$-1,000\leq x_0,y_0\leq 1,000,\ 1\leq a,b\leq 1,000$）

含义见题目描述

输出格式

一个实数 $c$ ，需满足 $x_0\leq c\leq x_0+a$ ，表示一条直线 $L:x=c$ ，可将三角形 $A$ 分成面积相等的两半。

输出结果保留 $5$ 位小数

输入样例1

0 0 1 1

输出样例1

0.29289

输入样例2

347 -685 868 194

输出样例2

601.23131

图示

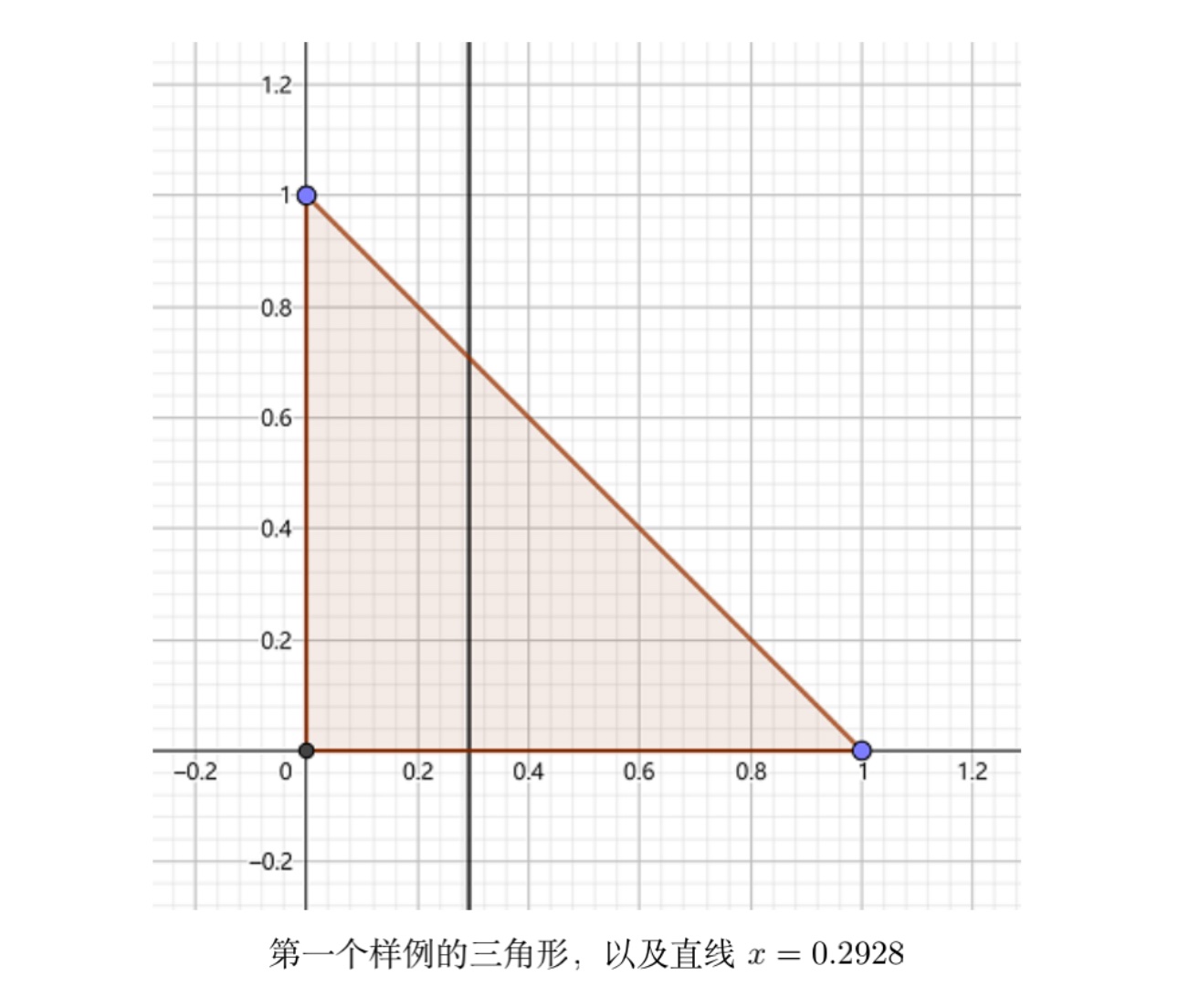
解的正确性判断

本题采用 Special Judge。

假设你给出的答案为 $c$ ，标准答案为 $d$ ，那么只有满足 $\frac{|c-d|}{\text{max}(1,|d|)}\leq 10^{-5}$ 时，你的答案才会被认为是正确的。如果你不太理解这里在说什么，那么你只需要按照题目的要求将结果保留 $5$ 位小数即可。

如果你wa了但过了大部分测试点，试着多输出几位小数。